tornis Šaha tornis 1 sek.  Uzdevums Uz kvadrātiskas rūtiņu lapas, kurai dažas rūtiņas var būt izgrieztas, novietota šaha figūra - tornis. Tornis vienā gājienā var pārvietoties uz jebkuru citu neizgrieztu lapas rūtiņu, kas ar sākotnējo atrodas vienā rindā vai kolonnā. Tornis nedrīkst pārvietoties pāri izgrieztai rūtiņai. Zīmējumā redzams, uz kurām rūtiņām tornis drīkst pārvietoties, ja pirms gājiena tas atrodas rūtiņā ar koordinātām (2;6). 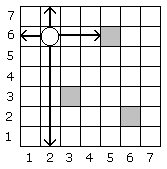Noskaidrot ar kādu mazāko gājienu skaitu tornis no sākotnējās rūtiņas var nokļūt līdz norādītai rūtiņai (ja tas vispār ir iespējams), pārvietojoties saskaņā ar iepriekšaprakstītajiem noteikumiem.    Ievaddati Faila tornis.in pirmajā rindiņā ir trīs naturāli skaitļi n, x un y (1<=n<=100, 1<=x, y<=n). Skaitlis n ir kvadrātiskās rūtiņu lapas malas izmērs, bet x, y - tās rūtiņas koordinātes, uz kuru jānokļūst tornim. Zināms, ka rūtiņa (x,y) nav izgriezta. Faila otrajā rindiņā ir viens skaitlis k (0<=k<=1000) - izgriezto rūtiņu skaits. Nākamajās k faila rindiņās ir skaitļu pāri xi, yi - i-tās izgrieztās rūtiņas koordinātes. Pieņemt, ka sākotnēji tornis atrodas rūtiņā ar koordinātēm (1,1), kas nav izgriezta.    Izvaddati Failā tornis.out jāizvada viens skaitlis - mazākais gājienu skaits, kurā tornis no sākotnējās pozīcijas var nokļūt līdz mērķim. Ja tornis nevar nokļūt līdz mērķim, tad jādrukā atbilde - NEVAR.    Piemērs tornis.in tornis.out 4 1 4 3 1 3 4 1 3 4 3     tornis.in tornis.out 2 2 2 2 1 2 2 1 NEVAR    Atsauces Uzdevums izmantots Latvijas 15.informātikas olimpiādes I (skolas) kārtā. Autori: M.Opmanis, A.Žogla Drukāšanai