taisnstn Taisnstūri un nogrieznis 3 sek.  Uzdevums Plaknē izvietoti N taisnstūri, kuru malas ir paralēlas koordinātu asīm. Taisnstūri var pārklāties, sakrist vai atrasties viens otra iekšpusē. Visu taisnstūru virsotņu koordinātas ir veseli nenegatīvi skaitļi un x koordināta nepārsniedz xmax un y koordināta nepārsniedz ymax. Ir novilkts nogrieznis AB, kura viens galapunkts atrodas punktā A(0, 0), bet otrs galapunkts B apmierina sekojošus nosacījumus: tā koordinātas ir veseli skaitļi; tas pieder vai nu nogrieznim [(0, ymax), (xmax, y max)] , vai arī nogrieznim [(xmax, 0), (xmax, ymax)]; Nogrieznis AB var krustot taisnstūrus (uzskatām, ka krustošanās ir arī tad, ja nogrieznis šķērso vienu taisnstūra virsotni). Uzrakstiet programmu, kas nosaka, kādu lielāko taisnstūru skaitu var krustot nogrieznis AB!    Ievaddati Teksta faila taisnstn.dat pirmajā rindā dotas trīs naturālu skaitļu xmax, ymax (0< xmax, ymax ≤109 ) un N (1≤N≤10000) vērtības. Katrā no nākošajām N rindām dots viena taisnstūra apraksts kā četru veselu skaitļu vērtības: apakšējā kreisā stūra koordinātas xapkr un yapkr un augšējā labā stūra koordinātas xaula un yaula . Starp katriem diviem blakus skaitļiem ir viens tukšumsimbols.    Izvaddati Teksta faila taisnstn.rez vienīgajā rindā jāizvada viens vesels skaitlis - lielākais taisnstūru skaits, ko var šķērsot nogrieznis AB.    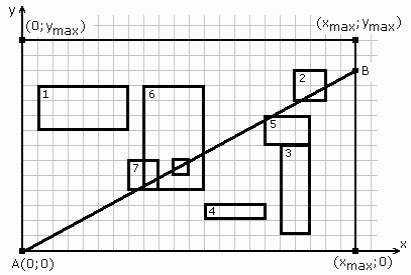Piemērs taisnstn.dat taisnstn.rez 22 14 8 1 8 7 11 18 10 20 12 17 1 19 7 12 2 16 3 16 7 19 9 8 4 12 11 7 4 9 6 10 5 11 6 5 Punkts B var būt (22,11) vai (22,12).    Atsauces Uzdevums izmantots Baltijas 10.informātikas olimpiādē Ventspilī 2004.gadā Drukāšanai