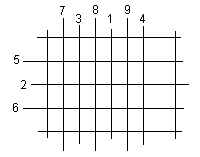
taisnst2 Taisnstūra pārsvītrošana 1 sek.  Uzdevums Kādu dienu Andris izdomāja spēli. Lai to iesāktu, viņš vispirms uz papīra lapas uzzīmēja divus paralēlu vertikālus un divus paralēlus horizontālus nogriežņus, tādējādi izveidojot taisnstūri kā parādīts zīmējumā. Pēc tam viņš sāka vilkt nākamos taisnes nogriežņus sadalot sākumā izveidojušos taisnstūri mazākos taisnstūros. Vispirms viņš novilka vertikālu nogriezni tieši pa vidu diviem vertikālajiem nogriežņiem, pēc tam tāpat viņš novilka horizontālu nogriezni tieši pa vidu diviem jau novilktajiem horizontālajiem nogriežņiem. Nākamos nogriežņus Andris vilka vispirms novelkot visus vertikālos nogriežņus tieši pa vidu jau novilktajiem vertikālajiem nogriežņiem, pēc tam – velkot horizontālus nogriežņus tieši pa vidu jau novilktajiem horizontālajiem nogriežņiem. Visi novilktie nogriežņi bija tik gari, ka šķērsoja visus otrā virzienā novilktos nogriežņus. Tādējādi Andris turpināja vilkt taisnes nogriežņus, kamēr bija novilkti tieši n taisnes nogriežņi. Uzrakstiet programmu, kas ievadītai n vērtībai nosaka, cik taisnstūrīšos beigās būs sadalījies sākumā uzzīmētais taisnstūris!  Ievaddati Teksta faila taisnst2.in pirmajā rindā ir dota naturāla skaitļa n vērtība- kopējais novilkto taišņu skaits (0<n<=90000).  Izvaddati Teksta faila taisnst2.out pirmajā rindā jāizvada viens naturāls skaitlis - mazo taisnstūru, kādos sadalīts sākotnējais taisnstūris, skaits.  Piemērs taisnst2.in taisnst2.out 9 28 Piezīme: Numurs pie nogriežņa nozīmē, kurš pēc kārtas šis nogrieznis tika novilkts. Drukāšanai