|
Korejā mazo varžu cheonggaeguri nerātnība ir leģendāra.
Tā ir laika gaitā iemantota slava, jo šīs vardītes mēdz naktī lēkt pāri jūsu rīsa laukam, nobradājot tajā stādus.
No rīta, ieraugot kuri no stādiem ir nobradāti, jūs vēlaties noteikt tās vardes ceļu, kuras izdarītie postījumi ir vislielākie.
Varde pāri rīsu laukam vienmēr lec taisnā līnijā, izdarot vienāda garuma lēcienus:

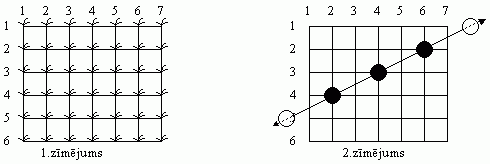
Jūsu rīsa lauka stādi ir sastādīti kvadrātveida režģa punktos kā redzams 1.zīmējumā, un vardes lec pilnībā pāri jūsu laukam,
sākot lēkt ārpus tā no vienas puses un beidzot lēkt lauka otrā pusē kā parādīts 2.zīmējumā:
Pāri rīsa laukam var lēkt daudzas vardes, izdarot lēcienus no viena stāda uz otru. Katrs lēciens beidzas uz kāda stāda un nobradā to, kā parādīts 3.zīmējumā.
Ievērojiet, ka viens stāds nakts laikā var dabūt ciest vairākkārt, ja tam nakts laikā uzlec vairākas vardes. Protams, jūs nevarat redzēt līnijas, kas norādītu katras vardes lēciena virzienu,
vai lēcienu pēdas ārpus rīsa lauka - 3.zīmējumā parādītajiem varžu lēcieniem jūs redzēsiet tikai 4.zīmējumā redzamo situāciju:
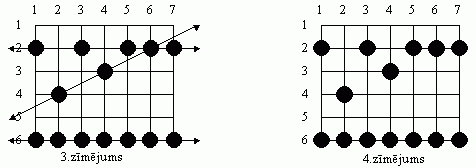
No 4.zīmējuma jūs varat rekonstruēt visus iespējamos ceļus, kā vardes varēja lēkt pāri jūsu laukam. Jūs interesē tikai tās vardes, kas ir nobradājušas vismaz trīs rīsa stādus savā ceļojumā pāri jūsu laukam.
Šādu ceļu sauksim par vardes ceļu. Tas nozīmē, ka trīs ceļi, kas redzami 3.zīmējumā, ir varžu ceļi (te ir arī citi iespējami varžu ceļi).
Vertikālais ceļš pa 1.kolonnu uz leju ir ceļš ar lēciena garumu 4, bet tajā ir tikai divi nobradāti stādi, un tādēļ mēs to nesaucam par vardes ceļu.
Uz diagonāla ceļa 2.rinda,3.kolonna; 3.rinda,4.kolonna un 6.rinda 7.kolonna ir trīs nobradāti stādi, bet nav iespējams atrast konstantu lēciena garumu un tāpēc arī tas nav vardes ceļš.
Ievērojiet, ka uz taisnes, kur atrodas vardes ceļš, var atrasties nobradāti stādi, kas nepieder šim vardes ceļam (piem. 4.zīmējumā, stāds 2.rindas 6.kolonnā attiecībā pret vardes ceļu pa 2.rindu)
un daži no nobradātajiem stādiem var nepiederēt vispār nevienas vardes ceļam.
Jūsu uzdevums ir uzrakstīt programmu, kas nosaka, kādu lielāko nobradāto stādu skaitu var saturēt vardes ceļš (jāaplūko visi iespējamie varžu ceļi).
4.zīmējumā redzamajā piemērā tie būtu septiņi stādi, kas pieder vardes ceļam pa 6.rindu.
Teksta faila vardes.in pirmā rinda satur divus naturālus skaitļus - lauka rindu skaitu R un lauka kolonnu skaitu C, 1 <= R,C <= 5000.
Otrā rinda satur vienu naturālu skaitli - nobradāto stādu skaitu N, 3 <= N <= 5000.
Katrā no nākošajām N rindām ir dots pa diviem naturāliem skaitļiem katrā - nobradātā stāda rindas numurs (1<= rindas numurs <= R) un
kolonnas numurs (1<= kolonnas numurs <=C), kas atdalīti ar tukšumsimbolu. Informācija par katru nobradāto stādu ir dota vienreiz.
Failā vardes.out jāizvada viens skaitlis - lielākais nobradāto stādu skaits uz viena vardes ceļa, ja kaut viens vardes ceļš eksistē.
Pretējā gadījumā jāizvada skaitlis 0.
| vardes.in | vardes.out |
6 7
14
2 1
6 6
4 2
2 5
2 6
2 7
3 4
6 1
6 2
2 3
6 3
6 4
6 5
6 7
|
7
|
Uzdevums izmantots Vispasaules 14.informātikas olimpiādē Yong-In (Koreja) 2002.gadā.
Drukāšanai
|

















