Taisnstūru zīmēšana

Uzdevums

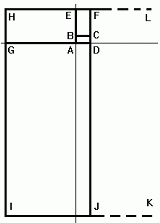
Taisnstūra ABCD virsotnes ir: A(0;0), B(0;1), C(k;1), D(k;0). Teiksim, ka šī taisnstūra numurs ir 1. Taisnstūra malu garumu attiecība ir 1:k, kā redzams zīmējumā.
Otrais taisnstūris tiek būvēts uz pirmā taisnstūra "Ziemeļu" šķautnes (BC), saglabājot iepriekšējo malu attiecību (1:k). Šis taisnstūris ir BEFC. |BC|:|BE|=1:k. Kopīgā taisnstūra AEFD "Rietumu" mala ir AE. Trešais taisnstūris tiek būvēts uz šīs malas AE, saglabājot iepriekšējo malu garumu attiecību (1:k). Šis taisnstūris ir AGHE. |AE|:|AG|=1:k. Tādā pat veidā nākošie taisnstūri tiek būvēti uz iepriekšējo kopīgo taisnstūru malām, saglabājot to pašu malu garumu attiecību un bāzes malu virzienu secību ("Dienvidu", "Austrumu", "Ziemeļu", "Rietumu", "Dienvidu", ...).

Uzrakstiet programmu, kura ievadītām veselu skaitļu k, x, y vērtībām,aprēķina un izvada tā taisnstūra numuru, kurš noklāj P(x;y)! Ja punkts P atrodas uz kāda taisnstūra malas vai virsotnē, tad uzskatīt, ka to noklāj taisnstūris ar mazāko iespējamo numuru.

Ievaddati

Teksta faila taisnst.in pirmajā ir dotas trīs veselu skaitļu k, x, y vērtības(1<k<100, -10⁹<x,y<10⁹). Starp katriem diviem blakus skaitļiem failā ir viens tukšumsimbols.

Izvaddati

Teksta faila taisnst.out pirmajā rindā jāizvada viens naturāls skaitlis - atrastā taisnstūra numurs.

Piemērs

taisnst.in	taisnst.out
3 0 1	1
taisnst.in	taisnst.out
2 7 -2	5

Atsauces