Taisnlīniju daudzstūra laukums

Uzdevums

Plaknē par taisnlīniju daudzstūri sauc tādu daudzstūri, kura malas ir vai nu horizontālas, vai vertikālas. Patvaļīga taisnlīniju daudzstūra malas var krustoties savā starpā. Vienkārša taisnlīniju daudzstūra malas savā starpā nekrustojas. Šajā uzdevumā aplūkosim patvaļīgus taisnlīniju daudzstūrus, kuriem ir spēkā šādas īpašības:

• vienā un tajā pašā punktā nevar atrasties vairākas daudzstūra virsotnes;
• katra daudzstūra virsotne ir vienas horizontālas un vienas vertikālas malas galapunkts;
• ja divas malas krustojas, tad viena no šīm malām ir horizontāla, bet otra - vertikāla - t.i., nekad savā starpā nekrustojas divi vertikāli vai divi horizontāli nogriežņi.

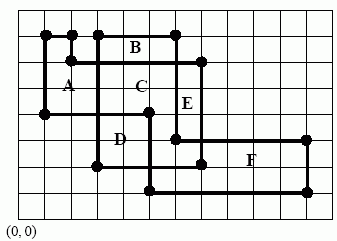
Vienas šāda taisnlīniju daudzstūra piemērs parādīts zīmējumā:

Šim daudzstūrim ir 14 malas un plakne tiek sadalīta sešos (ja neskaita ārējo plaknes daļu) vienkāršos taisnlīniju daudzstūros A, B, C, D, E un F. No šiem daudzstūriem vislielākais laukums ir daudzstūrim F.

Uzrakstiet programmu, kas nosaka lielākā vienkāršā taisnlīniju daudzstūra laukumu!

Ievaddati

Teksta faila tdstlauk.dat pirmajā rindā dota naturāla skaitļa N (4≤N≤1000) vērtība - taisnlīniju daudzstūra virsotņu skaits. Katrā no nākošajām N faila rindām doti divi nenegatīvi skaitļi x un y (0≤x,y≤10000) - vienas virsotnes x un y koordinātas. Starp skaitļiem ievaddatos ir viens tukšumsimbols.
Lai no datiem konstruētu taisnlīniju daudzstūri, katras divas blakus virsotnes jāsavieno ar taisnes nogriezni un pēdējā virsotne jāsavieno ar pirmo.

Izvaddati

Teksta faila tdstlauk.rez vienīgajā rindā jāizvada naturāls skaitlis - lielākā vienkāršā taisnlīniju daudzstūra laukums.

Piemērs

tdstlauk.dat	tdstlauk.rez
14 1 7 2 7 2 6 7 6 7 2 3 2 3 7 6 7 6 3 11 3 11 1 5 1 5 4 1 4	10

Atsauces