Mazais ČunSū rotaļājas ar metamajiem kauliņiem. Metamie kauliņi ir kubi, kuriem uz katras skaldnes vienreiz ir uzrakstīts kāds no naaturāliem skaitļiem no 1 līdz 6. Atšķirībā no parastajiem metamajiem kauliņiem, ČunSū kauliņiem pretējo skaldņu summa var atšķirties no 7. Dažādiem metamajiem kauliņiem skaitļi uz skaldnēm var būt izvietoti dažādi.
ČunSū no kauliņiem veido torni šādi: vispirms viņš paņem pirmo kauliņu un novieto to uz galda, tad ņem otro kauliņu un liek to uz pirmā kauliņa augšējās skaldnes tā, ka uz otrā kauliņa apakšējās skaldnes ir rakstīts tas pats skaitlis, kas bija uz pirmā kauliņa augšējās skaldnes. Pēc tam viņš turpina likt pēc kārtas visus pārējos kauliņus, ievērojot šo pašu principu - kārtējam kauliņam, kas tiek likts torņa augšā uz apakšējās skaldnes ir rakstīts tas pats skaitlis, kas bija rakstīts uz līdz šim pēdējā kauliņa augšējās skaldnes.
Kad tornis ir uzbūvēts, ČunSū vēlas noteikt, kāda var būt lielākā skaitļu summa uz vienas no torņa skaldnēm. Lai to izdarītu, katru kauliņu var pagriezt ap vertikālo asi (nejaucot torni!) par 90, 180 vai 270 grādiem.
Uzrakstiet programmu, kas dotam skaitļu izvietojumam uz metamo kauliņu skaldnēm nosaka, kāda lielākā skaitļu skumma var būt uz vienas torņa skaldnes!
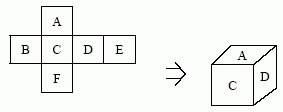
Teksta faila mekator.dat pirmajā rindā dots naturāls skaitlis N (1≤N≤10000) - metamo kauliņu skaits. Katrā no nākošajām N faila rindām dots pa viena kauliņa aprakstam kā sešu skaitļu A, B, C, D, E un F virkne, kas atbilst šo skaitļu izvietojumam uz metamā kauliņa skaldnēm kā redzams zīmējumā.

Starp katriem diviem blakus skaitļiem ievaddatos ir tukšumsimbols.
Teksta faila mekator.rez vienīgajā rindā jāizvada naturāls skaitlis - lielākā iespējamā skaitļu summa uz vienas torņa skaldnes.
| mekator.dat | mekator.rez | |
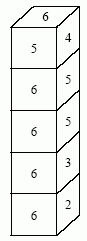
5 2 3 1 6 5 4 3 1 2 4 6 5 5 6 4 1 3 2 1 3 6 2 4 5 4 1 6 5 2 3 |
29 |
 |