Izlūku komanda nosūtīta izpētīt ceļu tīklu kādā mežonīgā apvidū, lai konstatētu un novērstu vētras radītos bojājumus. Plānā atzīmēti N krogi, kas sanumurēti no 1 līdz N. Krogus savieno pētāmie ceļi, kuru veikšanai nepieciešamais laiks un paredzētais kustības virziens ir zināmi. Zīmējumā parādīts piemērs ar N = 8.
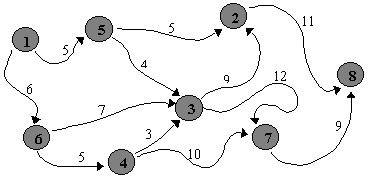
Visi izlūki ceļu sāk krogā 1 un pa dažādiem iespējamiem ceļiem dodas uz krogu N. Katrā ceļu sazarojumā grupa sadalās, un jaunās grupas vienlaicīgi dodas ceļā, lai izpētītu visus ceļa atzarus. Piemēram, no kroga 1 daļa izlūku dodas pārbaudīt ceļu uz krogu 5, kamēr pārējie orientējas uz krogu 6. Grupa, kas nonāk krogā 5, atkal sadalās divās, lai turpinātu ceļu uz krogiem 2 un 3. Izlūkgājiena dalībnieku maršruti ir izplānoti tā, lai katrā sazarojumā ierastos pietiekami daudz cilvēku vajadzīgo grupu izveidošanai.
Drošības apsvērumu dēļ grupa, kas pirmā nokļūst kādā krogā, nogaida, līdz ierodas grupas pa visiem pārējiem ienākošajiem ceļiem. Piemēram, ja izlūkgājiens no kroga 1 sākas laikā 0, tad pirmā grupa krogā 3 ierodas laikā 9 (caur krogu 5). Tai jāsagaida pārējās divas grupas, kas pa ceļam apmeklējušas krogus 4 un 6. Kad visas trīs izlūku grupas ieradušās, darbs turpinās divās grupās, virzoties uz krogiem 2 un 7.
Nevienu krogu nav iespējams apmeklēt vairākkārt, jo ceļi neveido ciklus. Tomēr garantēts, ka no sākuma kroga 1 var nokļūt jebkurā citā krogā un no jebkura kroga eksistē ceļš uz beidzamo krogu N.
Lai izlūku komandas vadītājs varētu veiksmīgi plānot savu atvaļinājumu, viņš vēlas noskaidrot dažus parametrus, kas raksturo izlūku darba efektivitāti.
Pirmkārt, nepieciešams aprēķināt minimālo laiku T, kas nepieciešams ceļu tīkla apsekošanai. Pieņem, ka darbs sākts laikā 0. Minētajā piemērā pēdējā izlūku grupa krogu 8 sasniedz ne ātrāk kā laikā T = 35.
Tā kā izlūku grupai, kas pirmā ierodas kādā krogā, jāsagaida pārējās grupas, tad noteikts laiks tiek pavadīts krogā, pārrunājot ceļā piedzīvoto. Gaidīšanas laiks ir starpība starp pirmās un pēdējās grupas ātrāko ierašanās laiku krogā. Piemēram, krogā 3 pirmā grupa ierodas laikā 9 (caur krogu 5), bet pēdējā grupa – laikā 14 (apmeklējot krogus 4 un 6), tātad gaidīšanas laiks šajā krogā ir 5. Jāaprēķina kopējais gaidīšanas laiks W, t.i., visu krogu gaidīšanas laiku summa.
Sevišķu interesi izraisa tie krogi, kuros pieļaujama uzkavēšanās arī pēc visu gaidāmo izlūku ierašanās, kas tomēr neiespaido kopējo misijas laiku T. Piemēram, grupa, kas krogā 5 nokļūst laikā 5, var atpūsties līdz laikam 10 un visur paspēt pievienoties pārējām. Izlūki, kas sapulcējas krogā 2 laikā 23, var vēl vienu laika vienību sagatavoties pēdējā ceļa posma veikšanai un pabeigt darbu tieši laikā 35. To krogu skaitu, kuros iespējama šāda rīcība, apzīmēsim ar D. Piemērā D = 2, jo nevienā krogā, izņemot 2 un 5, kavēšanās nav pieļaujama.
Uzrakstiet programmu, kas analizē dotu izlūkgājiena plānu un sniedz prasīto informāciju.
Teksta faila izluk.dat pirmajā rindā doti divi naturāli skaitļi N (2 ≤ N ≤ 100 – krogu skaits) un M (1 ≤ M ≤ 1000 – krogus savienojošo ceļu skaits), kas atdalīti ar tukšumsimbolu. Katrā no nākošajām M faila rindām doti trīs naturāli skaitļi, kas atdalīti ar vienu vai vairākiem tukšumsimboliem un raksturo vienu ceļu – sākuma krogs, beigu krogs un ceļā pavadāmais laiks (1 ≤ laiks ≤ 100).
Teksta faila izluk.rez vienīgajā rindā jāizvada trīs skaitļi, kas atdalīti ar tukšņiem – ātrākais darba veikšanas laiks T, kopējais gaidīšanas laiks W un krogu skaits D, kuros pieļaujama uzkavēšanās.
| izluk.dat | izluk.rez |
8 12 3 7 12 5 2 5 6 3 7 1 6 6 4 7 10 2 8 11 1 5 5 5 3 4 6 4 5 7 8 9 4 3 3 3 2 9 |
35 24 2 |