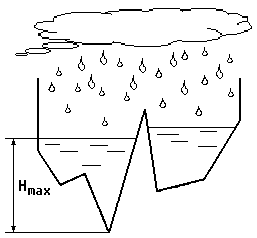
Uzņēmējs vēlas būvēt privāto mazo hidroelektrostaciju Gaujas ielejā. Upes ielejas reljefu var vienkāršoti attēlot šķērsgriezumā kā N posmu lauztu līniju ar virsotnēm (x0, y0), ..., (xN, yN), kur x0 < x1 < ... < xN, turklāt yi ≠ yj katriem i ≠ j. Pa kreisi no punkta x0 un pa labi no xN ieleju ierobežo ļoti augstas vertikālas klints sienas.
Ir zināms nokrišņu daudzums H vienā lietus periodā – t.i., ja reljefs būtu līdzens, tad pēc lietus visa ieleja būtu noklāta ar H metrus dziļu ūdens slāni. Bet, tā kā reljefs ir lauzta līnija, tad ūdens sakrājas padziļinājumos un veido atsevišķas ūdenstilpes.
Elektrostacijas jauda ir tieši atkarīga no ūdenskrātuves dziļuma. Uzņēmējs vēlas atrast izdevīgāko vietu elektrostacijas celtniecībai un noskaidrot plānojamo grunts pārvietošanas darbu lietderīgumu, tāpēc Jums jāuzraksta programma, kas dotam ielejas reljefam nosaka maksimālo dziļumu nokrišņu veidotajās ūdenstilpēs. Ekosistēmas apdraudējumu un saimnieciskās darbības ierobežojumus neievērot.
Teksta faila gauja.dat pirmajā rindā dots naturāls skaitlis N (1 ≤ N ≤ 100) un reāls skaitlis H (0 ≤ H ≤ 109) ar 3 cipariem aiz decimālā punkta. Katrā no nākošajām N + 1 faila rindām doti divi veseli skaitļi xi un yi, pie kam -10000 ≤ xi, yi ≤ 10000 visiem i no 0 līdz N. Skaitļi faila rindās atdalīti ar tukšumsimbolu. Beigās seko 100 rindas, kurās doti atbilžu varianti - katrā rindā pa vienam reālam skaitlim.
Starp dotajiem atbilžu variantiem jāatrod tas, kura vērtība ir vistuvākā meklētajam dziļumam Hmax. Teksta faila gauja.rez vienīgajā rindā jāizvada šīs atbildes kārtas numurs.
| gauja.dat | gauja.rez | |
7 7.000 -5 10 -3 4 -1 6 1 -4 4 17 5 3 9 5 12 15 14.3492 15.8448 15.8288 22.9323 ... (vēl 96 rindas) |
2 |
Piezīme: pareizā atbilde - apmēram 15.844619 |