Spoku pils

Uzdevums

Taisnstūrveida spoku pilij, kurā ir N*M istabas, kopš neatminamiem laikiem ir spēkā sekojoši likumi:
1. Ceļinieks no ārpuses var nonākt tikai istabā ar koordinātām (1;1)
2. Izkļūt no spoku pils var tikai tad, ja izdevies nonākt istabā ar koordinātām (N;M);
3. Katrā pils istabā uz grīdas ar krītu ir uzrakstīts maģiskais skaitlis - kāds naturāls skaitlis no 1 līdz 13;
4. Ceļinieks var iedomāties vienu no astoņiem virzieniem (paralēli pils ārmalām vai pa diagonālēm) un tūlīt kā vēja plēsts viņš tiek pārvietots iedomātajā virzienā tik istabas tālāk, kāds bija šajā istabā uzrakstītais maģiskais skaitlis. Ja tas nav iespējams (šajā virzienā tik daudz istabu nemaz nav), tad nekas nenotiek, un ceļiniekam, lai nokļūtu kur citur, jāiedomājas cits virziens.
5. Divreiz pēc kārtas pārvietoties vienā un tajā pašā virzienā nevar. Piemēram, ja ceļiniekam izdevies nokļūt pils (kurā ir 5*4 istabas un kuras plāns redzams zīmējumā) istabā ar koordinātām (3;3), tad ar vienu pārvietošanos ir iespējams nokļūt tikai istabās (1;1), (3;1), (1;3), (5;1) un (5;3). Savukārt, lai no istabas (3;2), izdarot tikai divas pārvietošanās, nokļūtu istabā (5;4) (tikai nonākot šajā istabā, var izkļūt no pils), nevar pirmajā reizē pārvietoties uz (4;3) (jo tad nākošreiz vajadzētu vēlreiz pārvietoties tajā pašā virzienā - ko darīt nevar), bet vispirms jāpārvietojas uz (2;1).
Uzrakstiet programmu, kas dotam pils plānam nosaka, kāds ir mazākais pārvietošanos skaits, lai ceļinieks no istabas (1;1) nokļūtu istabā (N;M), ievērojot visus pilī spēkā esošos likumus.

Ievaddati

Teksta faila pils.in pirmajā rindā dotas divu naturālu skaitļu N un M vērtības - istabu skaits plānā horizontālā un vertikālā virzienā (1<=N,M<=100).
Katrā no nākošajām M rindām doti N naturāli skaitļi - attiecīgajā istabu rindā uz grīdas uzrakstīto skaitļu vērtības.
Faila i+1-ajā rindā ir dota informācija par plāna i-to istabu rindu.
Katrā faila rindā starp katriem diviem blakus skaitļiem ir viens tukšumsimbols.

Izvaddati

Teksta faila pils.out pirmajā rindā jāizvada viens naturāls skaitlis - mazākais nepieciešamais pārvietošanos skaits.
Ja istabā ar koordinātām (N;M) dotajam pils plānam nonākt nav iespējams, teksta faila pils.out pirmajā rindā jāizvada vārds NEVAR.

Piemērs

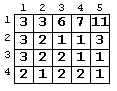
pils.in	pils.out
5 4 3 3 6 7 11 3 2 1 1 3 3 2 2 1 1 2 1 2 2 1	4