Tomātu kaste

Uzdevums

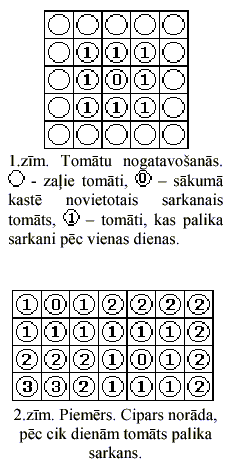
Dārznieks Krišs tomātus nogatavina lielās taisnstūrveida kastēs, kas sastāv no n*m (n rindas, m kolonnas) kvadrātveida nodalījumiem. Kastes rindas un kolonnas ir numurētas ar naturāliem skaitļiem pēc kārtas, sākot no 1. Katrā nodalījumā ir tieši viens tomāts. Katrs tomāts ir vai nu zaļš(negatavs), vai sarkans(gatavs). Krišs ir novērojis sekojošu lietu: ja zaļais tomāts atrodas blakus sarkanam (šo tomātu nodalījumiem ir vismaz viens kopīgs punkts), tad nākošajā dienā arī šis tomāts ir sarkans (skat 1.zīm.). Tādējādi, ieliekot kastē tikai pāris sarkanus tomātus, pēc dazām dienām visi kastē esošie tomāti būs sarkani. Otrajā zīmējumā redzams, kā trīs dienu laikā visi kastē esošie tomāti nogatavojās, lai gan sākumā tikai divi no tiem bija sarkani.
Tā kā tirgū iespējams pārdot tikai sarkanos tomātus, Krišs ir ieinteresēts uzzināt, pēc cik dienām ātrākais visi kastē esošie tomāti būs sarkani, ja tos kastē novieto vienlaicīgi ar zaļajiem.
Uzrakstiet programmu, kas dotai kastei un sarkano tomātu sākotnējam izvietojumam nosaka, ātrākais pēc cik dienām visi kastē esošie tomāti būs sarkani!

Ievaddati

Teksta faila kaste.in pirmajā rindā ir dotas trīs veselu pozitīvu skaitļu n (nodalījumu rindu skaits, n <=3*10⁴), m (nodalījumu kolonnu skaits, m <= 3*10⁴) un s (sarkano tomātu skaits kastē, s <= 30, s < n*m) vērtības. Nākošajās s faila rindās dots pa diviem naturāliem skaitļiem, kas norāda sarkanā tomāta rindas (r_i, 1 <= r_i <= n) un kolonnas (k_i, 1 <= k_i <= m) numuru. Starp katriem diviem blakus skaitļiem ir viens tukšumsimbols.

Izvaddati

Teksta failā kaste.out jāizvada viens naturāls skaitlis - mazākais dienu skaits, pēc kura visi kastē esošie tomāti būs sarkani.

Piemērs

kaste.in	kaste.out
4 7 2 1 2 3 5	3