3 1 2 3 0 0 0 0 1 0 1 0 1 0 0 0
3
Lai nonāktu pie dzīvā ūdens avota, ceļiniekam jāiziet cauri labirintam. Ne vienmēr tas ir izdarāms bez maģijas pielietošanas. Maģija ļauj ceļiniekam iet cauri labirinta sienām. Diemžēl maģiju var pielietot ierobežotu reižu skaitu, bet līdz avotam jānonāk pēc iespējas ātrāk.
Labirintam ir kvadrātveida forma un tas sastāv no N*N rūtiņām. Katru rūtiņu var viennozīmīgi noteikt ar tās koordinātām (rindas_numurs, kolonnas_numurs). Pa rūtiņu malām var būt izvietotas sienas.
Katrā brīdī ceļinieks var atrasties tieši vienā rūtiņā. Vienā solī ceļinieks var pārvietoties uz rūtiņu, kurai ar pašreizējo ir kopīga mala. Ceļinieks K reizes var iet cauri sienām un nevar iziet ārpus labirinta robežām.
Uzrakstiet programmu, kas nosaka, ar kādu mazāko soļu skaitu ceļinieks var nonākt rūtiņā ar koordinātām (P,Q), sākot ceļu rūtiņā (1,1)!
Teksta faila maglab.in pirmā rinda satur naturālus skaitļus N, K, P, Q (2<=N<=200, 0<=K<=250, 1<=P,Q<=N). Nākošā N-1 rinda satur pa N veseliem skaitļiem - horizontālo sienu pazīmes. Nākošās N rindas satur pa N-1 skaitlim - vertikālo sienu pazīmes. Pazīme ir 0, ja attiecīgajā vietā sienas nav, vai 1, ja siena ir.
Teksta failā maglab.out vienīgajā rindā jāizvada vesels skaitlis - mazākais soļu skaits, ar kādu ceļinieks var no rūtiņas (1,1) nonākt rūtiņā (P,Q).
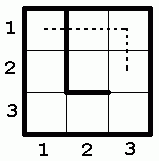
| maglab.in | maglab.out | |
3 1 2 3 0 0 0 0 1 0 1 0 1 0 0 0 |
3 |

|