Šoreiz izmantosim tikai pieca veida pentamino figūras:

Pentamino figūras veido no pieciem kvadrātiem, novietojot tos tā, ka katram kvadrātam ir kopīga mala ar kādu citu.
Šoreiz izmantosim tikai pieca veida pentamino figūras:

Sauksim tās par A, B, C, D un E veida figūrām. Katra veida figūrai viens kvadrāts ir iekrāsots citādi. Sauksim to par attiecīgā veida figūras galveno kvadrātu.
Kvadrātveida rūtiņu laukumā, kura izmēri ir 8*8 rūtiņas, izvietosim ne vairāk kā 10 iepriekšminētā veida figūras tā, lai katras figūras kvadrāti sakristu ar laukuma rūtiņām, un katra no figūrām pilnībā ietilptu laukumā. Figūras drīkst pārklāties. Figūras nedrīkst būt pagrieztas vai apgrieztas. Laukuma kolonnas ir sanumurētas no kreisās puses uz labo ar naturāliem skaitļiem no 1 līdz 8 pēc kārtas. Analoģiski no lejas uz augšu ir sanumurētas arī rindas.
Mēs vēlamies jau daļēji aizpildītajā laukumā novietot vēl vienu figūru tā, lai tā nepārklātos ar iepriekš noliktajām.
Jūsu uzdevums ir uzrakstīt programmu, kas nosaka, cik dažādās laukuma vietās šo figūru var novietot.
Teksta faila pentam3.in pirmā rinda satur naturālu skaitli N, 1 <= N <= 10, kas apzīmē uz laukuma izvietoto pentamino figūru skaitu.
Katrā no nākošajām N faila rindām tiek dotas kādas figūras apraksts formā
burts kolonnas_numurs rindas_numurs, kur burts norāda attiecīgās figūras veidu (A,B,C,D vai E), bet kolonnas un rindas numurs norāda laukuma rūtiņu, kuru noklāj šīs figūras galvenais kvadrāts. Starp burtu un kolonnas numuru, kā arī starp kolonnas numuru un rindas numuru ir viens tukšumsimbols. Pēc tam faila nākošajā rindā ir dots viens burts (A,B,C,D vai E), kas norāda tās figūras veidu, kuru vēlamies novietot laukumā bez pārklāšanās.
Teksta faila pentam3.out vienīgajā rindā jāizvada viens vesels skaitlis - vietu skaits laukumā, kur iespējams izvietot figūru.
| pentam3.in | pentam3.out | |
5 A 2 5 D 5 7 B 7 6 D 8 1 E 4 6 E |
6 |
Derīgās vietas atzīmētas ar krustiņiem: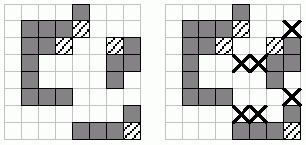
|