Cipariem no 0 līdz n (1<=n<=9) ir definēta operācija @, kuras rezultāts arī ir cipars robežās no 0 līdz n.
Piemēram, ja n=2, tad @ var aprakstīt ar sekojošas tabulas palīdzību, attēlojot visas iespējamās operācijas a@b vērtības
(kur a un b - cipari robežās no 0 līdz 2):
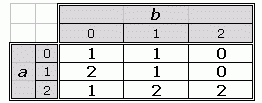
Kā redzams, šajā gadījumā operācija nav nedz komutatīva, jo 0@1 = 1, bet 1@0 = 2 , nedz asociatīva (0@1) @2 = 0, bet 0@ (1@2)=1.
Ja dota izteiksme x1@x2@x3@x4@...xk-1@xk (kur katrs xi ir robežās no 0 līdz n),
tad tās vērtību aprēķina no kreisās puses uz labo tāpat kā izteiksmes
(...(((x1@x2)@x3)@x4)@...xk-1)@xk vērtību, sākot ar visdziļāk iekļautajām iekavām -
vispirms aprēķina x1@x2 rezultātu r1, pēc tam aprēķina r1@x3 rezultātu, utt.
Mainot iekavu izvietojumu sākotnējā izteiksmē, tās rezultāts var mainīties.
Piemēram, ja dota izteiksme 1@1@1@1@0, tad piemērā redzamajai operācijai @ izteiksmes (1@ (1@1)) @ (1@0) vērtība ir 0, bet (((1@1) @1)@1) @0 vērtība ir 2.
Uzrakstiet programmu, kas dotam n, ar tabulu uzdotai operācijai @ un ciparu virknei x1x2x3x4...xk-1xk katram veselam skaitlim t (0<=t<=n) nosaka, vai izteiksmē x1@x2@x3@x4@...xk-1@xk iespējams salikt iekavas tā, lai šīs izteiksmes vērtība būtu t.
Failā opera.in pirmajā rindā dota naturāla skaitļa n vērtība (1<=n<=9).
Nākošajā n+1 faila rindā ir uzdota operācija @.
Katrā no šīm rindām ir n+1 cipars: faila i+2-ās rindas j+1-ais cipars ir operācijas i@j rezultāts (0<=i<=n,0<=j<=n).
Starp katriem diviem blakus cipariem failā ir viens tukšumsimbols.
Faila n+3-ajā rindā ir dota ciparu virkne x1@x2@x3@x4@...xk-1@xk
bez atdalošiem tukšumiem.
Virknes garums ir vismaz divi un ne vairāk kā 250 cipari.
Teksta failam opera.out jāsatur tieši n+1 rinda.
Katram t (0<=t<=n) faila t+1-ajā rindā jābūt vārdam "VAR", ja iekavas dotajā izteiksmē iespējams salikt tā, lai izteiksmes vērtība būtu t,
vai "NEVAR", ja šādi iekavas izvietot nav iespējams.
| opera.in | opera.out |
2 1 1 0 2 1 0 1 2 2 11110 |
VAR NEVAR VAR |