Šaha tornis - 2

Uzdevums

Uz bezgalīgas rūtiņu lapas, kurai dažas rūtiņas var būt izgrieztas, novietota šaha figūra - tornis.
Lapas rindas un kolonnas ir sanumurētas pēc kārtas ar veseliem skaitļiem.
Kolonnas ir numurētas no kreisās puses uz labo, bet rindas no lejas uz augšu.
Tornis vienā gājienā var pārvietoties uz jebkuru citu neizgrieztu lapas rūtiņu, kas ar sākotnējo atrodas vienā rindā vai kolonnā.
Tornis nedrīkst pārvietoties pāri izgrieztai rūtiņai.

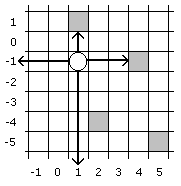
Zīmējumā redzams, uz kurām rūtiņām tornis drīkst pārvietoties, ja četras lapas rūtiņas ir izgrieztas un tornis pirms gājiena atrodas rūtiņā ar koordinātām (1;-1).
Kā redzams, šajā gadījumā tornis var pārvietoties bezgalīgi tālu horizontālā virzienā pa kreisi vai vertikālā virzienā uz leju.

Noskaidrot, ar kādu mazāko gājienu skaitu tornis no vienas norādītas rūtiņas var nokļūt līdz otrai norādītai rūtiņai (ja tas vispār ir iespējams), pārvietojoties saskaņā ar iepriekšaprakstītajiem noteikumiem.

Ievaddati

Faila tornis2.in pirmajā rindiņā ir doti četri veseli skaitļi x₁, y₁, x₂, y₂, kas atdalīti ar tukšumsimboliem.
x₁ (kolonnas numurs) un y₁ (rindas numurs) norāda tās rūtiņas koordinātes, kurā tornis atrodas sākumā, bet x₂ un y₂ analoģiskā veidā norāda tās rūtiņas numuru, kurā tornim jānokļūst beigās.
Zināms, ka -10⁹<=x₁, y₁, x₂, y₂ <= 10⁹ un ka neviena no šīm divām rūtiņām nav izgriezta.
Faila otrajā rindā dots naturāls skaitlis n - izgriezto rūtiņu skaits (n<=1000).
Faila nākošajās n rindās katrā doti divi veseli skaitļi, kas atdalīti ar tukšumsimbolu - vienas izgrieztās rūtiņas koordinātas.
Faila i+2-ajā rindā (1<=i<=n) ir dots i-tās izgrieztās rūtiņas kolonnas numurs p₁ (-10⁹<= p₁<= 10⁹) un rindas numurs q₁(-10⁹<= q₁ <=10⁹).

Izvaddati

Failā tornis2.out vienīgajā rindā jāizvada viens vesels skaitlis - mazākais gājienu skaits, kurā tornis no vienas norādītas rūtiņas var nokļūt līdz otrai norādītai rūtiņai.
Ja tornis nevar nokļūt līdz otrai norādītajai rūtiņai, tad faila vienīgajā rindā jāizvada vārds "NEVAR".

Piemērs

tornis2.in	tornis2.out
1 -1 5 -4 4 1 1 5 -5 2 -4 4 -1	3
tornis2.in	tornis2.out
10 11 5001 -4733 5 5001 -4732 5001 -4734 1 1 5000 -4733 5002 -4733	NEVAR

Atsauces